子どもに分かる割り算・分数の意味

ジュース3本を4人で分けるとき、「3÷4＝3/4本」は何を表している？

子どもの割り算・分数の教え方でいちばん大事なのは、
「式の意味を自分のことばで説明できること」です。

このページでは、ジュース3本を4人で分けるという身近な場面を使って、
「式の意味をイメージできる力」を子どもが身につけていくコツをまとめています。
クリックすると該当箇所へ移動できる目次を用意しました。

1｜親子で話すときのヒント

ジュース3本を4人で分ける、というテーマで、「公平に分ける」ってどういうことか、
「3÷4」「3/4」はどんな意味をもつ数なのかを、YouTubeショート動画でまとめました。

YouTube動画はこちら

第1回で伝えたいのは、式を見たときに「これって、どんな場面のこと？何をしているのか？」と、その意味を言葉で説明できて、頭の中で場面が浮かぶことの大切さです。

算数は「答えを当てる教科」ではなく、どのように答えを導き出したかというプロセスを学ぶ教科。その視点を、親子で一緒に共有していきましょう。

少し先で学ぶ方程式の世界では、知りたい答え（数や量など）を x や y といった文字に置きかえて式を立て、その式にそって手順通りに計算していくだけで答えが導かれます。

一見すると「式が勝手に考えてくれている」ように見えるので、
「この式は、どんな場面で、何と何の関係を表しているのか？」
「今、自分はこの式を使って何をしているのか？」
という“式の意味”を意識しないまま、解くだけで終わってしまいやすくなります。

もちろん、計算できること自体も大事です。
8÷4＝2 と解けること、3÷4＝0.75 と計算できることは、算数の「土台」になります。
でもそれだけでなく、
「8÷4（＝2）は、どんな場面の、何を表す数？」
「3÷4（＝3/4, 0.75）は、どんな場面の、何についての数？」
と聞かれたときに、式が表している場面やイメージ、式の意味を自分のことばで説明できる力も、計算と同時に育てていきたい大切なポイントです。

だからこそ、
「この式はいったい何を表している数？」
「どんな場面で、ひとり分がどれくらいになる話？」
「もし絵にするなら、どんな図やイラストになる？」
といったことを、自分の言葉で説明できて、イメージとして思い描けることが大切です。
今回は、そのための「最初の一歩」として使ってもらえるようにまとめています。

2｜まず「3÷4」を“ことば”にしてみる

いきなり計算ではなく、式の意味から入ります。
3÷4
＝ ジュース3本を、4人で同じだけ分けたときの、1人あたりの本数

ここで押さえておきたいのは、
割り算（÷）は、全体を同じぶんずつ分けて、そのときの1人分／1つ分を決めることだという点です。「÷」という記号は、その考え方をひとまとめに表しているだけです。

割り算は、いつも
・全体がいくつあるか
・いくつに分けるか（何人・何こに分けるか）
・1人あたり、1つあたりを考えている
この3つで成り立っています。

3｜8÷4 と 3÷4 は「考え方の型」が同じ

子どもは、どうしても
8÷4＝2
3÷4→割り切れない
と、「割り切れるかどうか」や「答えの見た目」だけに目がいきがちです。

そこで、一度 8÷4 を使って、式の意味に引き戻します。
8÷4
＝ ジュース8本を、4人で同じだけ分けたときの、1人あたりの本数

3÷4 と見比べると、
「÷4」は「4人で分ける」
「1人あたりの量」を求めている
という考え方の流れは、どちらも同じです。

違うのは、全体の本数が「8本か3本か」だけ。
8本なら、1人2本という整数で書ける。
3本なら、1人3/4本という分数で書くことになります。

8÷4 も 3÷4 も、どちらも「1人あたりの“分（ぶん）”全体を4人で分けたときの、1人あたりの“取り分”」を表す、同じ「考え方の型」の式です。
ただし、実際の量は、8÷4 は「1人2本」、3÷4 は「1人3/4本」と違う、ということを押さえてあげましょう。

4｜「自分が分ける／もらう立場で考える」ことの意味

「自分が分ける側だったら？」「自分がもらう側だったら？」という問いは、
“1人あたり”に注目させてくれる大事な学びの問いです。
親がこうした問いかけをくり返し一緒に使っていくことで、
少しずつ、子ども自身も問題を見たときに自分で問いを立てられるようになっていきます。

たとえば、こんなふうに言い換えられます。
「4人のうちの誰か一人に注目してみようか？」
「あなたが、その一人だったら、どれくらいもらえる？」
「あなたが、分けてあげる人だったら、どれくらいあげる？」

つまり、
「分ける側」でも
「もらう側」でも、どちらでも、
“一人”あたりに注目して、その分を考える
ことが、大切です。

ジュースの場面であれば、
3本のジュース
4人の子ども
その中の一人分のジュースを考える
この「一人分のジュース」が、まさに3÷4 が表している数です。

5｜ここで出てくる「1/4本」のイメージ

ジュース3本のうち、とりあえず1本に注目してみます。
「この1本を、4人で同じだけ飲むとしたら、どう分ける？」
と聞くと、多くの子は、
「同じ大きさに4つに分ける」
「1つずつあげる」
と言います。

この「1本を4つに分けた1つぶん」が、1/4本です。
1/4本 ＝ 1本を4つに同じ大きさで分けたうちの1つぶん

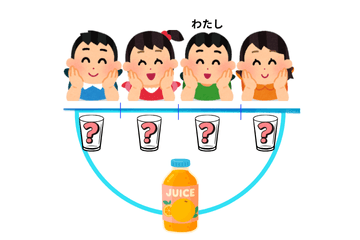
まずは、この具体的なイメージを親子で共有しておくことが大切です。

6｜3人が同じことをすると「3/4本」になる

ジュースを持っている3人（Aさん・Bさん・わたし）が、
それぞれ自分の1本を、同じように4つに分けて、みんなに1つずつ配ります。
1人分を集めるために、まず空のコップを1つ用意しておきます。

その空のコップ1つに、
Aさんから 1/4本ぶん
Bさんから 1/4本ぶん
わたしから 1/4本ぶん
が注がれるので、
1/4 ＋ 1/4 ＋ 1/4 ＝ 3/4本
となります。

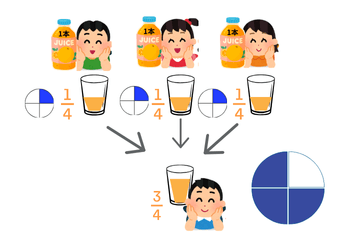
ここで、よく出る質問がこれです。
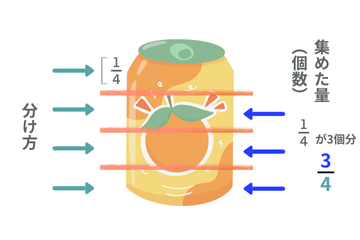
「なんで分母（4）はそのままで、分子だけ3になるの？」

このときに伝えたいのは、
分母（4）… どう分けたか
「1本を4つに分けた」という分け方はずっと同じだから、4のまま。
分子（3）… そのかたまりがいくつ集まったか
1/4本が3つ集まったから、3になる。
ということです。

分母＝分け方
分子＝集まった個数
この場面を使って、分母と分子の役割にも軽く触れておくと、分数の理解がスムーズになります。

7｜「割り切れない」モヤモヤへの返し方

子どもは、こう感じます。
「8÷4は2でスッキリなのに、3÷4は変。割り切れないから気持ち悪い。」

この「気持ち悪さ」の正体は、
これまで習ってきた“整数だけの世界”では表しきれない数が出てきた、ということです。

ここで大人から返してあげたいメッセージは、
「今までは“1, 2, 3 …”という整数で世界を見てきたけれど、
実はそのまわりには、まだたくさんの“数の仲間たち”がいるんだよ。」
ということです。

たとえば親として押さえておきたい豆知識として、次のような「定義」があります。
（くわしくは、この記事の最後にある 豆知識コーナー でも整理しています。）

・3÷4 は「3本を4人で分けたときの、一人あたりの取り分」を表す数
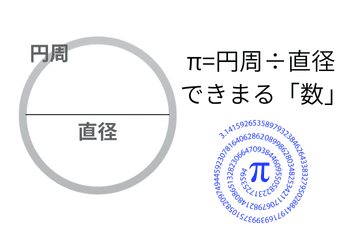
・π（パイ:円周率）は「円周 ÷ 直径」で定義される数
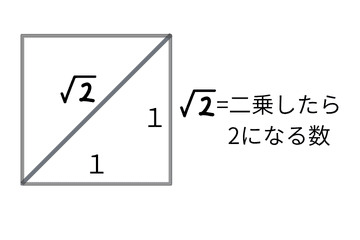
・√2 は「二乗したら2になる数」で定義される数（無理数）

どれも、まず「この数は何を表しているのか」という意味（定義）が先にあり、
0.75 や 75% といった小数や百分率は、
その同じ意味を“別の書き方で表したもの”です。

3÷4 もおなじで、
・「ジュース3本を4人で分けたときの、一人あたりの取り分」という意味（定義）が先にあり、
・そのあとに、その同じ取り分を 0.75 や 75% といった形で書ける、という順番です。

と伝えてあげると、「割り切れない＝おかしい」ではなく、
“整数では書けないけれど、ちゃんと意味のある数”として受け止めやすくなります。

8｜「量が書いていないのに、どうして分けられるの？」－前提を自分で決めて考える力

よくある疑問がこれです。
「1本にどれくらい入っているか、書いてないよね？」

ここで大事なのは、
算数は「前提条件を決めた世界」で考える学問だということです。

数学は、「こういう前提で考えます」と条件を置いた瞬間に成立します。
逆に言えば、前提条件なしに数学は成り立ちません。

じつは算数レベルでも、子どもは暗黙に次のような前提を採用しています。
・1本を4等分できるとみなす
・量を測るものさしがあるとみなす
・4つに分ければ4つは同じ大きさになるとみなす

しかし子どもは現実の経験も同時に持っているため、
「本数は本来割れない」「ジュースの量は厳密には測れない」など、
現実と数学の世界がごちゃまぜになり、混乱が生まれます。
この混乱は正常な反応です。

この問題では、次のような前提を置いています。
・3本のジュースは、どれも同じ量が入っている
・その量は、同じものさしで量れる
・量は連続的に分けられるとみなす

この前提があるからこそ、
「1本を4つに分けた1つぶん＝1/4本」と考えてよく、
それを3本から集めれば「1/4が3つで3/4本」と言えるわけです。

親が添えられる一言としては、
「3本とも同じ量で、同じように量れるって“決めている”から、こういう分け方ができるんだよ。」
と伝えてあげると、
子どもが“現実の世界”と“算数の世界”の切り替えをつかみやすくなります。

ここで押さえておきたいのは、
算数では「どんな前提で考えているか」を自分で設定できることが、とても大切だということ。
前提を置く力が育つと、分数だけでなく文章題・比例・割合など、
これから出てくる多くの単元の理解がスムーズになります。

→ 「前提を決める力」が算数の理解を深くする詳しい解説はこちら

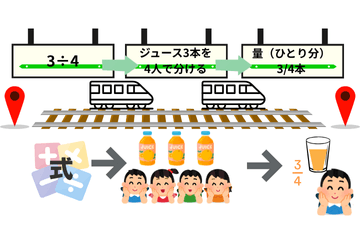
3÷4という式から出発して、ジュースの場面をイメージしながら、
最後に「一人分の量＝3/4本」にたどり着くまでの道のり

9｜家庭でできる「式をことばにする」練習

例題1：8÷4の式は何を表しているか？
例：8切れのピザを4人で同じだけ分けたときの、1人あたりの枚数を表している
この場合は「2枚」と整数で書ける

例題2：3÷4の式は何を表しているか?
例：3本のジュースを4人で同じだけ分けたときの、1人あたりの本数を表している
この場合は「3/4本」になる

例題3：12÷3は何を表しているか？
例：12個のお菓子を3つの皿に同じ数ずつ分けたときの、1皿あたりの個数
この場合は「4個」と整数で書ける

例題4：5÷2は何を表しているか？
ことば：5本のジュース（または5枚のお菓子）を2人で同じだけ分けたときの、1人あたりの本数（枚数）
この場合は「2と1/2本」（2と1/2枚）になる

どの式でも共通しているのは、
「ひとつあたり・一人あたり」を表す数になっているという視点。
親子で「この式はどんな場面？」と話すだけで、
子どもが自分で問いを立て、式からストーリーを思い描く力が伸びていきます。

📚 豆知識：分けることから広がっていく「数の世界」

ここからは、読み物としてのコーナーです。
親が背景として知っておくと、子どもへの声かけがやりやすくなります。

1｜「公平に分ける」からはじまった割る・分数

紀元前1600年ごろ、古代エジプトで書かれたリンド数学パピルス（Rhind Mathematical Papyrus）
という算数の文書には、パンや穀物を何個か用意しそれを人数で分け、
1人ぶんを分数で表すといった問題が並んでいます。

つまり、かなり古い時代から、
「みんなで公平に分けるときの1人ぶん」を表すために、分数が使われていた
ということです。

ジュース3本を4人で分ける、という問題も、
この流れの中にある、現代の一例だと言えます。

2｜π や √2 も「ことばで定義された数」

少し先の話ですが、
中学・高校に進むと、子どもたちは
π（円周率）、√2
のような数に出会います。

どちらも、「きれいな小数」で書ききることはできません。
どこまでも続いてしまう小数（無理数）です。

でも数学では、
π は「円周 ÷ 直径」で定義される数
√2 は「二乗したら2になる数」で定義される数
として扱われます。

ここでのポイントは、
どんな数も、「こういう性質をもつ数ですよ」という
ことばでの定義が先にある
ということです。

3÷4 も同じで、
「ジュース3本を4人で同じだけ分けたときの、1人あたりの本数」
という ことばの定義 が先にあって、
その内容を 0.75 や 3/4、75% といった数で表している、という順番です。

💡 考え方のひと口アドバイス

どんな式にも、「この式は何を表す数か」という定義があります。
8÷4 も 3÷4 も、
「（何本かのジュース）や（何枚かのピザ）を4人で同じだけ分けたときの、1人あたりの量」
を表す式。
違うのは、全体の本数（枚数）が8か3かだけです。

整数・分数・小数・π・√2…
どれも「こういう性質をもつ数ですよ」ということばでの定義をもった“数の仲間”です。
子どもが式を見たときに、「これは、どんな場面のどんな量のこと？」と
自分のことばで言えるようになることが、計算力と同じくらい大事な土台になります。