算数はセンスやひらめきじゃない。中学受験算数の良問で鍛える「着眼力」の育て方

“考え方”をどう育てるか?に興味のある方は、
算数シンキングエンジン|“つまずく前”を鍛える6つの思考トレーニング
もぜひご覧ください。
1.この問題で伝えたいこと――公式だけ知っていても、三角形は見えてこない
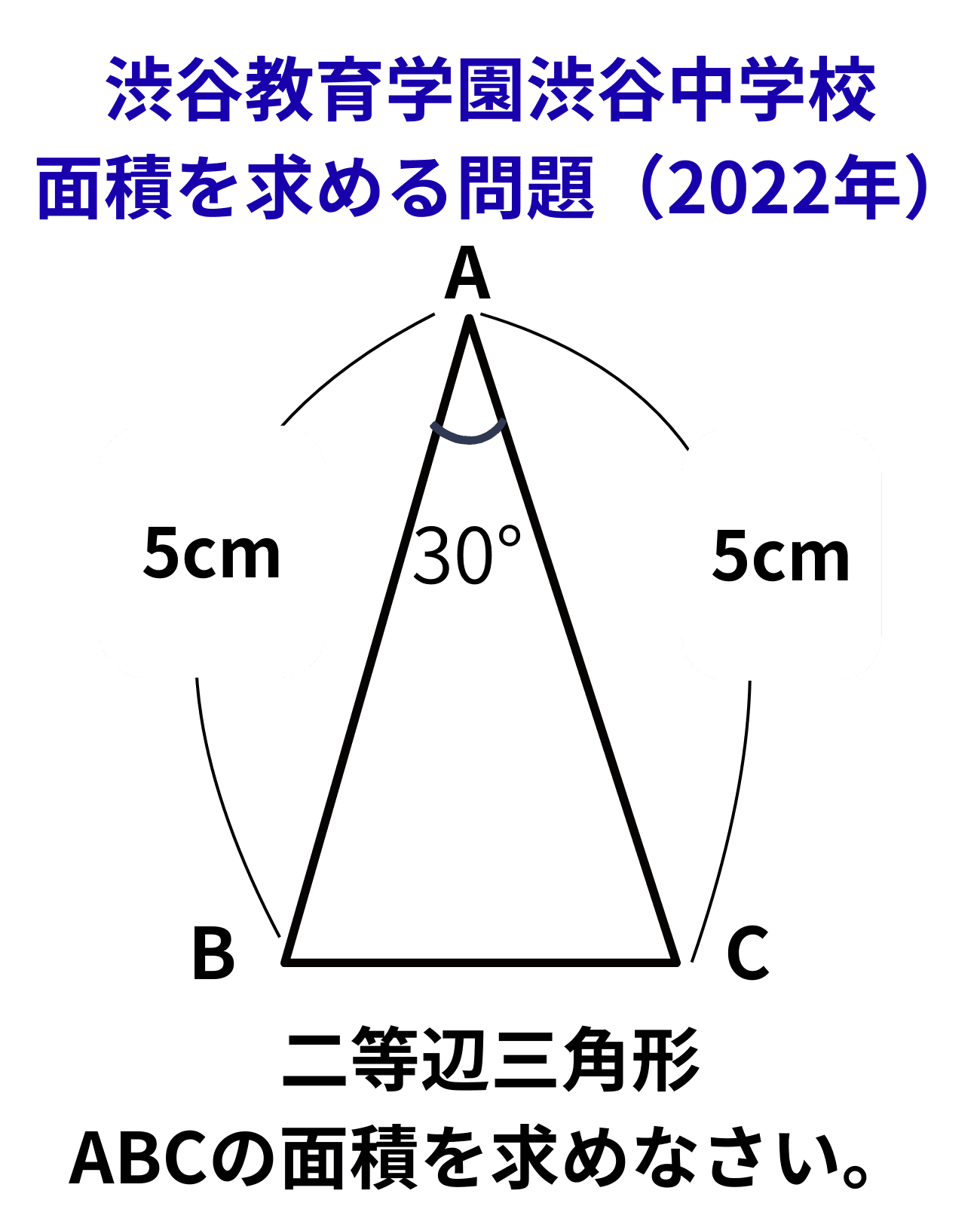
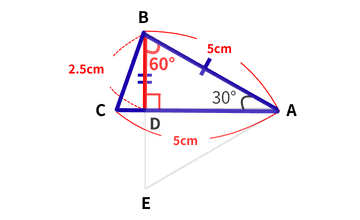
この問題は、「三角形の面積を求める問題」ですが、三角形の面積の公式(面積=底辺×高さ÷2)を知っているだけでは解けません。
また、中学受験の対策では、
- 30°‐60°‐90°三角形の「辺の比」を暗記しておくこと
- それを根拠に「30°の向かいは斜辺の半分だよ」と説明すること
といった、その知識を覚えているかどうかでしか解けないような教え方も少なくありません。
一方で、こうした問題に向き合うとき、保護者の方のなかには、
- 「うちの子にはセンスがないのかも」
- 「こういうのは、ひらめきがある子じゃないと無理なのかな」
と、不安になったり、少しあきらめに近い気持ちを抱えている方も多いと思います。
でも、ここでお伝えしたいのは、「センス」や「生まれつきのひらめき」だけで決まるわけではないということです。
この図を前にして、「どこを底辺と見るか」「どう図を見直すか」「なぜ正三角形をつくろうと思えるのか」といった力は、もともと持っている才能ではなく、図の見方や考え方を練習することで育てていける力です。
SheSTEMでは、単に知識を覚えることではなく、
- 図形をタテ・ヨコ・ナナメから捉え直す力
- 「あ、こう見直したら分かりやすい!」という気づきにつながる思考力
を大事にしています。
この記事では、この問題を、「知識だけではなく、図の見方や着眼点の大切さ」が伝わる代表的な一問として取り上げながら、センスやひらめきだけに頼らない算数の力の育て方をお伝えしていきます。
2.考え方の道すじと、子どもの頭の中で起きていること
| ステップ | 解き方 | 子どもの頭の中で起きていること/つまずきポイント/求められる力 |
|---|---|---|
| 0 |
問題の条件を確認する
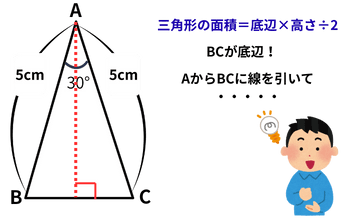

|
頭の中で起きていること
つまずきポイント 求められる力
|
| 1 |
ステップ① 三角形を「くるっと倒して」、長さが分かる辺を底辺にする

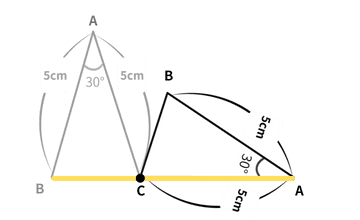
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 2 |
ステップ② Bから底辺に「まっすぐ」線をおろす(高さを作る)
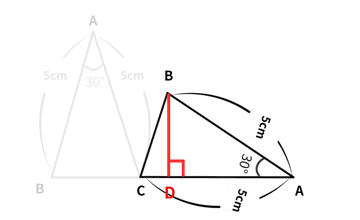
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 3 |
ステップ③ 角度を利用して「60°」を見つける
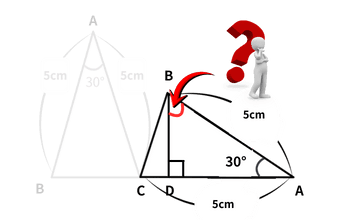
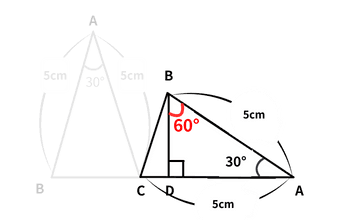
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 4 |
ステップ④ 60°から「正三角形」を作る
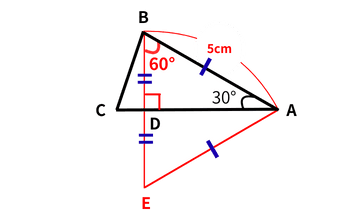
|
頭の中で起きていること
つまずきポイント:60°は見えても、「正三角形を作る」発想が出ない 求められる力
|
| 5 |
ステップ⑤ BDが「正三角形の一辺の半分」だと分かる
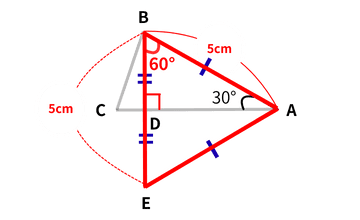
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 6 |
ステップ⑥ 面積の計算
|
頭の中で起きていること
つまずきポイント 求められる力
|
3.この問題で働いている SheSTEM の「6つの思考OS(思考の土台)」
SheSTEMでは、算数の問題を「正解・不正解」だけで見るのではなく、
その裏でどんな力が働いているかを
SheSTEMの「6つの思考OS(思考の土台)」
で整理しています。
今回の問題で特に働いているのは、次の6つです。
- ① センサーモニター力
-
いつものやり方(AからBCに高さをおろす)では高さが出てこない、という行き詰まりやモヤモヤに気づく力。
「あれ、おかしいな」と感じられることが、「別の見方を試してみよう」という出発点になります。 - ② 空間根拠力
-
三角形をくるっと回しても同じ三角形であり、面積も変わらないと理解する感覚。
図形の向きや見え方に惑わされず、「中身は同じ形だよね」とつかまえられる力です。 - ③ 構造視覚推論
-
高さをおろしたあとの三角形ABDの角度から60°を見つけ、
「ここに正三角形が作れそうだ」と図の中のパターン(構造)を読み取る力。
BDが正三角形の辺のちょうど半分になっていることに気づくのも、この力です。 - ④ 実行ロジック機能
-
「図を回した方が良さそう」「正三角形が作れそう」という気づきを、
実際に手を動かして描いてみるところまでつなげる力。
頭の中のアイデアを、行動の手順に落とし込む「段取り力」です。 - ⑤ 数量・数理の中核
-
三角形の内角の和が180°であること、正三角形の性質、5を半分にすると2.5になることなど、
数や式の意味を理解して扱う力。
ただ公式を暗記するのではなく、「この180は何の和?」「この2.5は何の半分?」と結びつけて考えます。 - ⑥ 意味表現力
-
「どうして図を回したのか?」「どうしてBDが2.5cmだと言えるのか?」を、
図を指さしながら自分の言葉で説明する力。
この力が育つと、単に“なんとなく解けた”ではなく、「分かった!」がしっかり自分のものになります。
親が「ちゃんと教えなきゃ」と構えるというより、
子どもの「気づき」や「考えようとしている時間」に付き合ってあげることが、
目の前のテストの点だけではなく、
新しいことに出会ったときに「自分で考えてみよう」「まずやってみよう」と一歩踏み出せる土台になっていきます。
それは、算数や理科の問題に向き合うときはもちろん、
本を読むとき、人の話を聞くとき、友だちや家族と意見を交わすときなど、
これから子どもが出会っていく、さまざまな学びと経験を支える
「考える力のOS」そのものです。
こうしたOSを、“テスト対策”ではなく考え方そのものを鍛える教材として形にしたのが、 SheSTEMの 算数シンキングエンジン です。
4.なぜ「3辺の比の暗記」に頼りすぎるのはよくないのか?
中学受験の対策では、
90°・60°・30°の直角三角形では、30°の向かい側のいちばん短い辺の長さは斜辺の半分になる、
という性質を、「この形が出てきたらこう解くんだよ」という解き方の“型”や“定石”として、
そのまま暗記させてしまうことがよくあります。
暗記していることやテクニック自体が悪いわけではありません。
ただ、それ「だけ」でしか解けないようになってしまうと、本来この問題で経験してほしい
「きれいな二等辺三角形をまずは正攻法で考えてみる」
→「うまくいかない“行き詰まり”に気づく」
→「図の見方や底辺の取り方を変えてみる」
というプロセスを飛ばしてしまいます。
その結果、子どもたちの中に、次のような問題が起こりやすくなります。
❶ 「見た瞬間にパターンを探す」クセがつく
- 問題を見る。
- 「これはあのパターンかな?」と“当てはめ先”を探す。
- パターンにハマらない問題が出た瞬間、手が止まる。
この問題でいえば、
本来なら、まずはきれいな二等辺三角形をそのまま眺めて
「AからBCに高さをおろしたらどうなるかな?」と考えてみて、
「あれ、高さの長さが出てこないぞ」という行き詰まりに気づく流れがあります。
ところが、最初から
「あ、30°があるから、30°‐60°‐90°だ」
→ 比を当てはめて高さを出す。
という解き方だけになり、
- なぜ60°が出てきたのか。
- なぜ正三角形を作ると分かりやすいのか。
といった図の構造を見る目が育ちません。
❷ 図の向きや形が少し変わると、急に「別世界の問題」になる
たとえば、
- 三角形の向きが上下逆だったり、
- 30°の位置がちょっと違っていたりすると、
「いつもの図と違う」と感じた瞬間に、テクニックが使えなくなります。
本来は、図を少し回したり、底辺の取り方を変えたりするだけで、
セクション2で見たのと同じ考え方で解けるのに、
「これは習っていないパターン」
と判断してしまいがちです。
❸ 「考え方の楽しさ」「気づきの快感」を経験しにくい
この問題のように、
- 自分で図を回してみる。
- 高さをおろして対称性を見つける。
- 正三角形をくっつけて「あ、ここが半分なんだ」と気づく。
というプロセスには、
「あ、分かった!」という小さな成功体験がたくさん詰まっています。
テクニックだけで処理してしまうと、
「なんとなく分かったような、分からないような」
という感覚のまま、
「覚えさせられたことを使うだけの算数」になってしまいがちです。
6.保護者としてできる声かけのヒント
最後に、動画や問題を見たあとに、
ご家庭でかけられると良い「一言」をいくつか挙げておきます。
- 「底辺って、必ず“下の線”じゃないとダメなのかな?」
- 「この図のままだと、高さどこからどこか分かりやすい?分かりにくい?」
- 「もし紙をくるっと回してもいいとしたら、どんな向きにしたら解きやすくなりそう?」
- 「60°が出てきたとき、何か思い出す形あるかな?」(→正三角形につなげる)
- 「どうして、ここが“半分”って分かったの?」
こうした問いは、
- 正解を当てさせるため、というより
- 子ども自身の「気づき」を言葉にしてあげるためのものです。
それが、そのまま SheSTEMの思考のOS(思考の土台)
- センサーモニター力
- 空間根拠力
- 構造視覚推論
- 実行ロジック機能
- 数量・数理の中核
- 意味表現力
を育てるトレーニングになります。
算数の“ひらめき”はセンスではなく、考え方の積み重ねで育ちます。
SheSTEMの教材 算数シンキングエンジン では、
中学受験の「良問」で問われるような着眼力や論理的思考を、楽しく体系的に鍛えることができます。


