算数オリンピックの良問で鍛える:対称性×立体感覚×数の性質――迷子にならない整理のしかた

問題
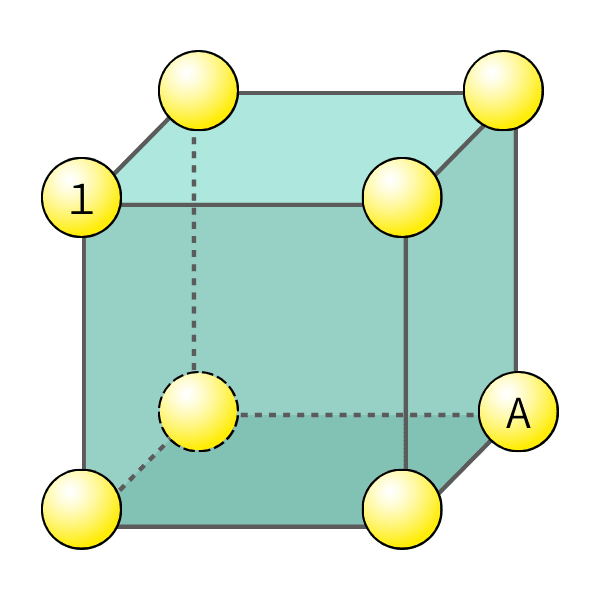
立方体の8つの頂点に、1〜8の数字を1回ずつ入れる。
立方体のどの面も、4つの頂点の数字の和が同じになるように入れるとき、図のAに入る数字を求めよ。
ただし、1は(図の場所に)すでに入っている。
(答えは1つとは限らない)
関連動画(同じ問題を別ルートで解説)
この記事では、この問題を「整理して解く」ルートで解説しています。 でも、同じ問題でも、解き方は1つではありません。 動画では、別の角度から解き進めていきます。
同じ問題をいろんな角度で研究しておくと、 次に似た問題に出会ったときに、迷子になりにくくなります。 「問いを立てる」「立て直す」練習にもつながります。
動画で見る(YouTube)別タブで開きます
見どころ
- 迷子になりやすい理由を整理
- 動く情報を減らす「2つの問い」
- 数の条件 → 立体として成立するかで確認
考え方の道すじと、子どもの頭の中で起きていること
この問題は、立方体の8つの角に1〜8を1回ずつ入れ、どの面も「4つの角の和」が同じになるようにするものです。
ねらいは、立体の基本構造(角・辺・面の関係)をつかみ、対称性や数の性質(数え上げ・場合分け・排除)で整理していく力を育てることにあります。
※スマートフォンでは、横にスライドしてご覧いただけます。
| ステップ | 解き方 | 頭の中で起きていること/つまずきポイント/求められる力 |
|---|---|---|
| 0 |
条件を整理する(立体の見取り図を頭に置く)
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 1 |
1つの面の和を先に決める(18)
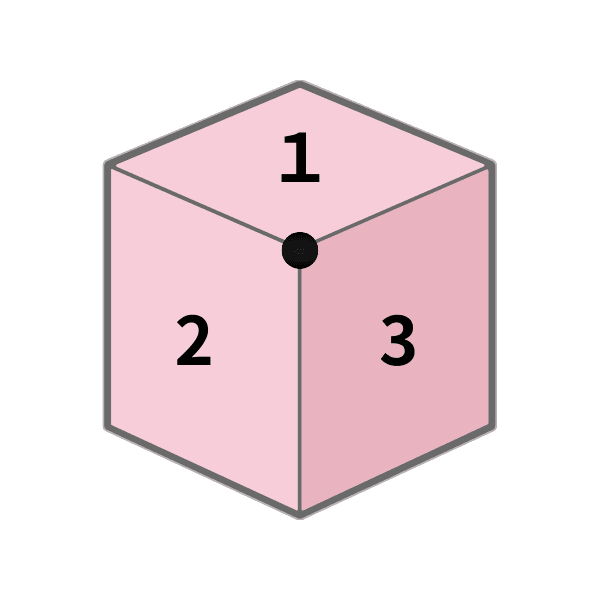
各頂点の数字は、面の合計づくりに「3回」登場します |
頭の中で起きていること
つまずきポイント 求められる力
|
| 2 |
「1を含む面」3枚にズームする(見る範囲を一気に狭める)
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 3 |
「1を含む面」の候補を作る準備(残り3つの和=17)
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 4 |
合計17の3つ組を「漏れなく」出す(最大の数に注目)
(1)8が入る場合
(2)7が入る場合(8を使わない場合)
合計17の3つ組(全部) (2,7,8) (3,6,8) (4,5,8) (4,6,7) 1を足して「1を含む面」の候補(4つ組)にする (1,2,7,8) (1,3,6,8) (1,4,5,8) (1,4,6,7) |
頭の中で起きていること
つまずきポイント 求められる力
|
| 5 |
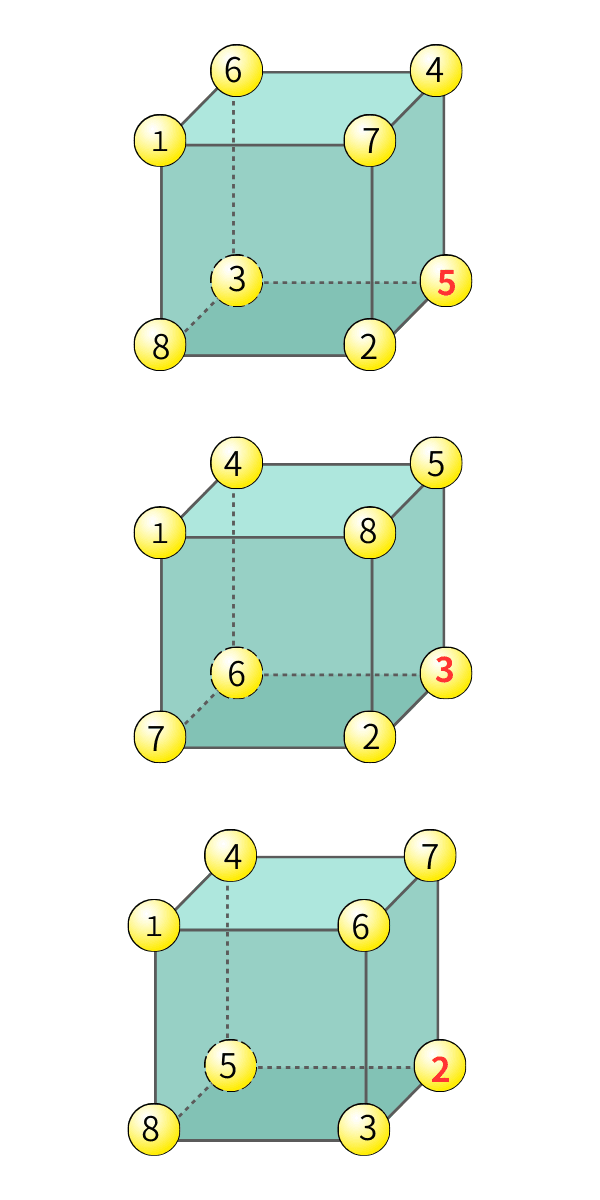
立体のルールで「同時に成り立たない」を排除する
残り2面の選び方(3通り)
|
頭の中で起きていること
つまずきポイント 求められる力
|
| 6 |
Aは「残った数字」で決まる(配置を完成させない)
3通りを調べる
まとめ:A=2,3,5 |
頭の中で起きていること
つまずきポイント 求められる力
|
答え
A=2、3、5
もう一度:押さえるポイント
- 面の和は必ず18
1+2+3+4+5+6+7+8=36。各頂点の数字は面に3回登場するので、6面の合計は36×3=108。よって1面は108÷6=18。 - 「1を含む面」は必ず3枚
頂点には面が3枚集まるため、1の周りの3面に注目して考える。 - 1を含む面は「残り3つが17」
面の和が18なので、1を含む面では1以外の3つの和は18−1=17。 - 合計17の3つ組は4通りだけ
上限(6+5+4=15)から、必ず7か8が入る。結果として、(2,7,8)、(3,6,8)、(4,5,8)、(4,6,7)。 そこに1を足して、1を含む面の候補は4つ:
(1,2,7,8)、(1,3,6,8)、(1,4,5,8)、(1,4,6,7)。 - 立体のルールで「同時に無理」を消す
1の周りの3面が共通にもつ角は1だけ。だから、8が3面すべてに同時に入る形は作れない。
その結果、8を含まない (1,4,6,7) は必ず入る。 - Aは「1の周りの3面に出ない数字」
Aは1と向かい合う角なので、1を含む3面には入らない。よって、選んだ3面に出てこない数字がA。
3通りを調べると、A=5、3、2となる。

関連動画(同じ問題を別ルートで解説)
この記事では、この問題を「整理して解く」ルートで解説しています。 でも、同じ問題でも、解き方は1つではありません。 動画では、別の角度から解き進めていきます。
同じ問題をいろんな角度で研究しておくと、 次に似た問題に出会ったときに、迷子になりにくくなります。 「問いを立てる」「立て直す」練習にもつながります。
動画で見る(YouTube)別タブで開きます
見どころ
- 迷子になりやすい理由を整理
- 動く情報を減らす「2つの問い」
- 数の条件 → 立体として成立するかで確認
今回の問題で育つ「思考のOS」
この問題は、立体の図を見て終わりではありません。
立方体の構造(角と面の関係)を手がかりにしながら、数の性質(同じ和・登場回数)で条件を固定し、
組み合わせ(漏れなく候補を出して、ありえないものを消す)で整理して答えにたどり着きます。
- 空間根拠力:「1つの角には面が3枚集まる」「Aは1と向かい合う角」など、立体の位置関係を頭に置き続ける力。
- 数量・数理の中核:36×3や108÷6のように、合計を“回数”で捉えて条件を一気に決める力。
- 構造視覚推論:「ペア→3つ組→4つ組」と部品として組み立て、候補の構造を崩さずに整理する力。
- 実行ロジック機能:ズームする(1の周りに絞る)→場合分けする→排除する、の手順で迷子にならずに進める力。
「できた/できない」よりも、「どこに着目して、どう整理したか」を言葉にできると、同じタイプの問題に強くなります。
さらに、図形が苦手になりやすい子ほど、「頭の中で回す」練習を短く積み重ねると変わりやすいです。
1回10分・全12回(4週間)の回転力トレーニングで、目印の固定→更新→戻り方の型を身につけます。


