平均って何で割る?「2で割る」が危ない理由

アプリ思考とOS思考でわかる“平均の正体”
「平均」と聞くと、つい“真ん中っぽい数字”を出したくなります。
でも平均は、ただの「真ん中」ではありません。
公式や計算手順を否定しないまま、「何を求めているのか」から組み立てるOS思考で、
平均の落とし穴を整理します。
問題
同じ距離を移動します。
行き:時速40km 帰り:時速60km
このとき、平均の速さは何km/hでしょう?
よくある答え:50km/h(でも違います)
「速さが2つある。だから平均は (40+60)÷2 で50。」
この発想は自然です。数字が2個あると、2で割りたくなります。
でもこの問題で、平均は50になりません。
この問題は、YouTubeでも同じ題材で解説しています。
目と耳で一緒に整理したい方は、こちらもどうぞ。
ここが今回の核心:
算数の式は、ただの記号ではなく「何をしているのか」を表す“ことば”です。
平均の問題は、計算より先に、式の意味(何を1つ分として見ているか)を押さえると一気に整理できます。
アプリ思考とOS思考とは?
アプリ思考
公式・計算・型。
速く正確にする“道具”
OS思考
何を1つ分にするか決める。
意味から組み立てる“土台”
アプリは大事です。
ただ、OSがないと「何を計算すればいいか」が決まらず、アプリが起動できないことがあります。
平均の速さは、まさにそれが起きやすい分野です。
OSを起動する合言葉
平均 = 合計 ÷ いくつ分
そして大事なのは、「いくつ分って、何の1つ分?」を決めること。
よくある誤解:「速さ=距離÷時間を覚えてたら解ける」
たしかに「速さ=距離÷時間」は正しい公式です。
でも平均の問題では、ここで止まりやすいです。
理由はシンプルで、速さ=距離÷時間は「1時間あたり、どれだけ進むか」を表す式だからです。
つまり速さの数字には最初から「時間1つ分」の意味が入っています。
例えば、
時速40km=1時間で40km進む
時速60km=1時間で60km進む
です。
だから「平均の速さ」は、全体として“1時間あたり何km進んだことになるか”で考える必要があります。
- 距離はどれ?(片道?往復?)
- 時間はどれ?(行き?帰り?合計?)
- 「平均」の対象は何?(全体としての速さを1つにしたい)
公式は“道具”ですが、その道具に入れる「距離」と「時間」を同じ全体にそろえる必要があります。
この「全体を定義する」仕事がOS思考です。
よくある指導の落とし穴:公式で誤解を上書きしてしまう
よくある解説はこう言います。
「速さ=距離÷時間だから、平均は(40+60)÷2じゃない」
式自体は正しい。けれど、この言い方だけだと学びが“アプリ追加”で終わることがあります。
起きがちな流れ
- もともとの誤解:平均=(40+60)÷2
- そこに新しい公式(速さ=距離÷時間)が追加される
- でも「距離ってどれ?時間ってどれ?」が決まらない
- 結果:入れる数字を当てにいく(理解が増えない)
本当に教えるべき1手目は、公式ではなく、何を求めているのか(全体は何か)を決めることです。
つまり、式を「ことば」として読み、何を表す式なのかを先に押さえることです。
正しい考え方:平均の速さ=全体の距離 ÷ 全体の時間
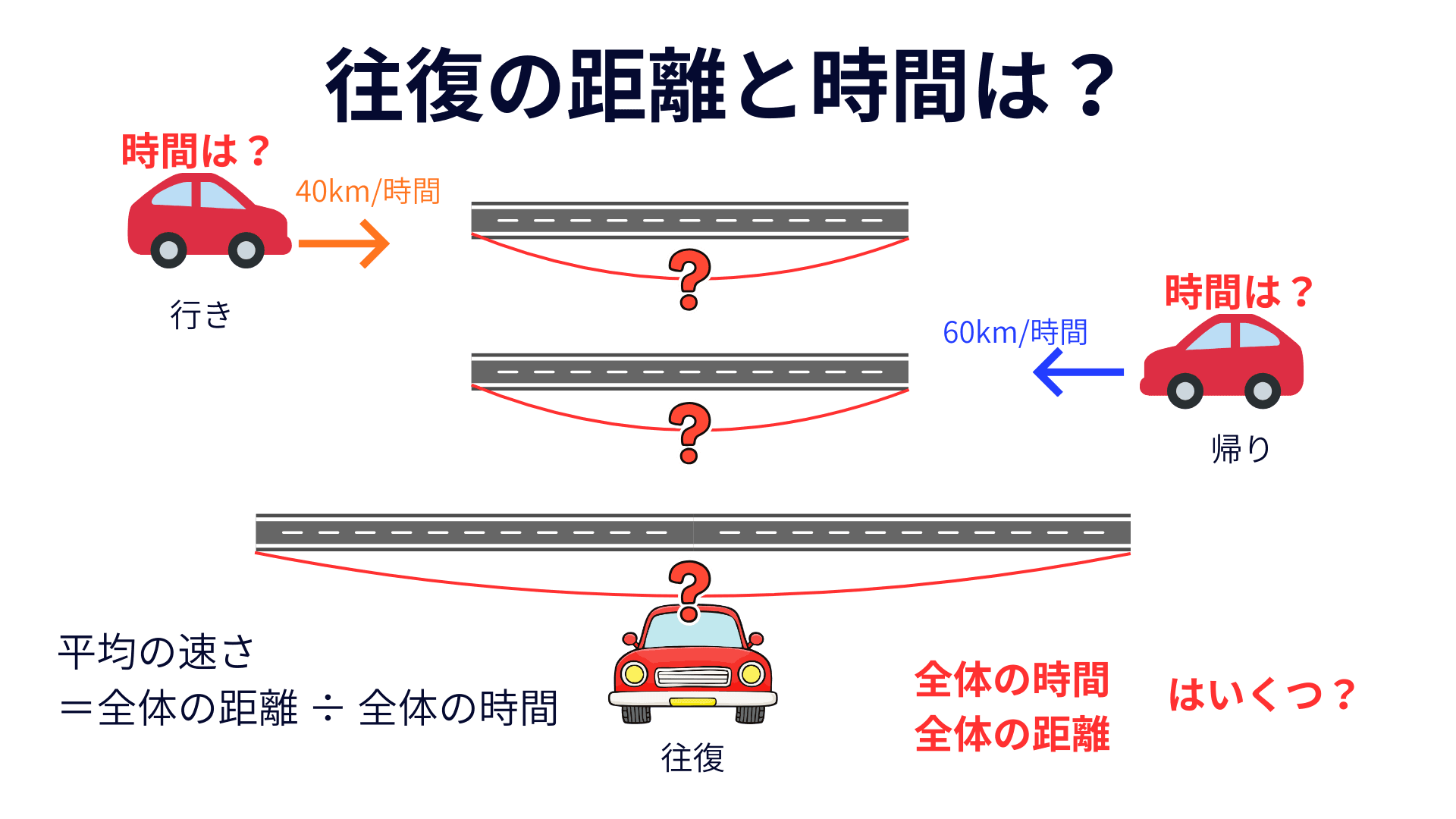
平均の速さは、「行き」と「帰り」をバラバラに見ません。
行って帰ってくる“ひとまとまり(往復)”として考えます。
ひとまとまりにすると、見るのは2つだけ。
往復の距離と往復の時間。
だから 平均の速さ=(往復の距離)÷(往復の時間) です。
OSの一言:
平均は“真ん中”ではなく合計÷いくつ分。速さの平均は全体の距離÷全体の時間で考える。
解き方:距離を仮に置く(最短ルート)
ここが大事:
同じ道のり(片道の距離)が同じなら、距離を何kmに決めても平均の答えは変わりません。
なぜなら、距離を2倍にすると、かかる時間も2倍になります(時間は距離に比例)。
だから 速さ=距離÷時間 の「距離」と「時間」を両方2倍にしても、速さは同じまま。
つまり、片道の距離は 計算しやすい数に自分で決めてOK です。
そして往復の距離は、片道×2です。
平均の速さは 「全体の距離 ÷ 全体の時間」。
だから先にやるのは、行きの時間+帰りの時間で全体の時間を作ること。
そのために、片道の距離は計算しやすい数に仮に置いてOK(ここでは120kmとします)。
距離の全体は往復なので 片道×2。
最後に 速さ=距離÷時間 を使って、平均の速さを出します。
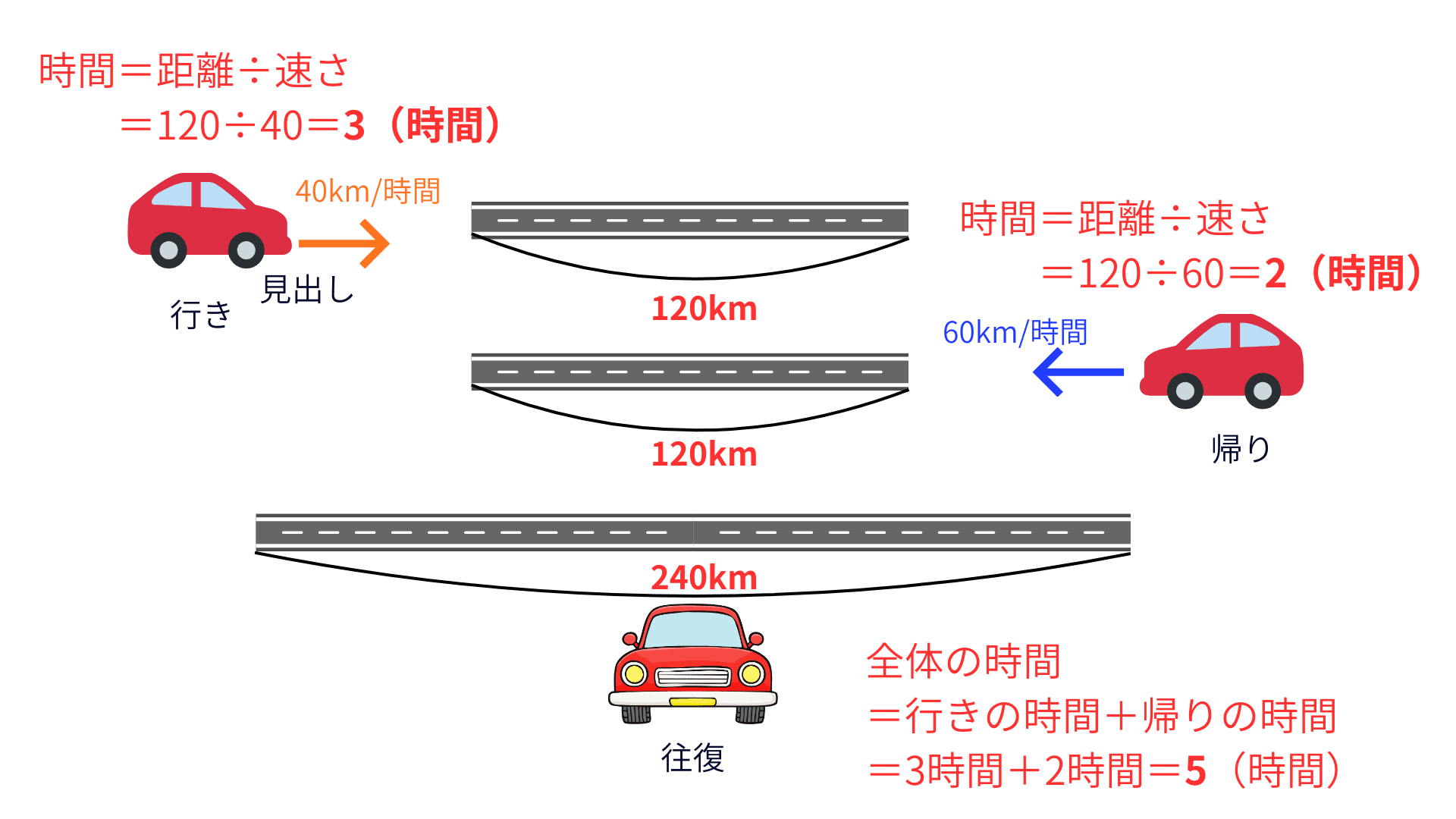
OSの確認:
距離(全体)と時間(全体)をそろえてから、速さ=距離÷時間(アプリ)を使う。
- 行きの時間:120 ÷ 40 = 3時間
- 帰りの時間:120 ÷ 60 = 2時間
- 全体の時間:3 + 2 = 5時間
- 全体の距離:120 + 120 = 240km
- 平均の速さ:240 ÷ 5 = 48km/h
答え:48km/h
50ではありません。
なぜ「2で割る」と間違えるの?
(40+60)÷2 は、40と60を同じ重みで平均しています。
これは、言い換えると「40km/hで走った時間」と「60km/hで走った時間」が同じ長さだったとみなしているのと同じです。
でも今回の条件は同じ距離を行って、同じ距離を帰ること。
速さが違うのに距離が同じなら、かかる時間は同じになりません。
遅い40km/hの方が長い時間走るので、全体としての平均は40寄りになります。
そしてここでもう一度。
速さ=距離÷時間 は「1時間あたりどれだけ進むか」という意味の式です。
平均の速さは、全体として“1時間あたり何km進んだことになるか”を1つにすること。
だから、足して2で割るのではなく、全体の距離÷全体の時間で決めるのが正しい、ということです。
今日のまとめ:アプリも大事。OSがあると、もっと使える
- アプリ(公式・計算)は、速く正確にしてくれる
- OS(意味・全体・1つ分)は、何を計算するかを決めてくれる
- 式は“ことば”。何を表している式なのか、意味から読めると強い
アプリは道具。OSは使い方。両方そろうと強い。
家庭で使える「OSを育てる声かけ」3つ
- 「何の平均? 1つ分は何?」
- 「全体ってどこからどこまで?」
- 「この式は、何をしてる式?」
「うちの子はアプリ思考?OS思考?」
学び方を整理したい方は、こちらの診断記事もどうぞ。
6つの思考のOS
SheSTEMでは、考える力を「6つのOS」として育てます。
公式(アプリ)を使いこなすための“基本ソフト”です。
- センサーモニターOS:手を動かして、気づくOS
- 空間根拠OS:どこがどこにつながるか、場所で考えるOS
- 構造ビジュアルOS:形のルール(しくみ)を見つけるOS
- 実行ロジックOS:順番を決めて、ためして直すOS
- 数量・数理OS:どれくらい?を数字でつかむOS
- 意味表現OS:わかったことを言葉で説明するOS
6つの思考のOSについて、詳しくはこちらで解説しています。
6つの思考のOSを詳しく見る
